Code 9: End to End Bayesian Workflows

Code 9: End to End Bayesian Workflows#

This is a reference notebook for the book Bayesian Modeling and Computation in Python

The textbook is not needed to use or run this code, though the context and explanation is missing from this notebook.

If you’d like a copy it’s available from the CRC Press or from Amazon. ``

import pandas as pd
import arviz as az

import matplotlib.pyplot as plt
import pymc3 as pm
import numpy as np
import theano.tensor as tt
from scipy import stats, optimize

np.random.seed(seed=233423)
sampling_random_seed = 0

az.style.use("arviz-grayscale")
plt.rcParams['figure.dpi'] = 300 

Making a Model and Probably More Than One#

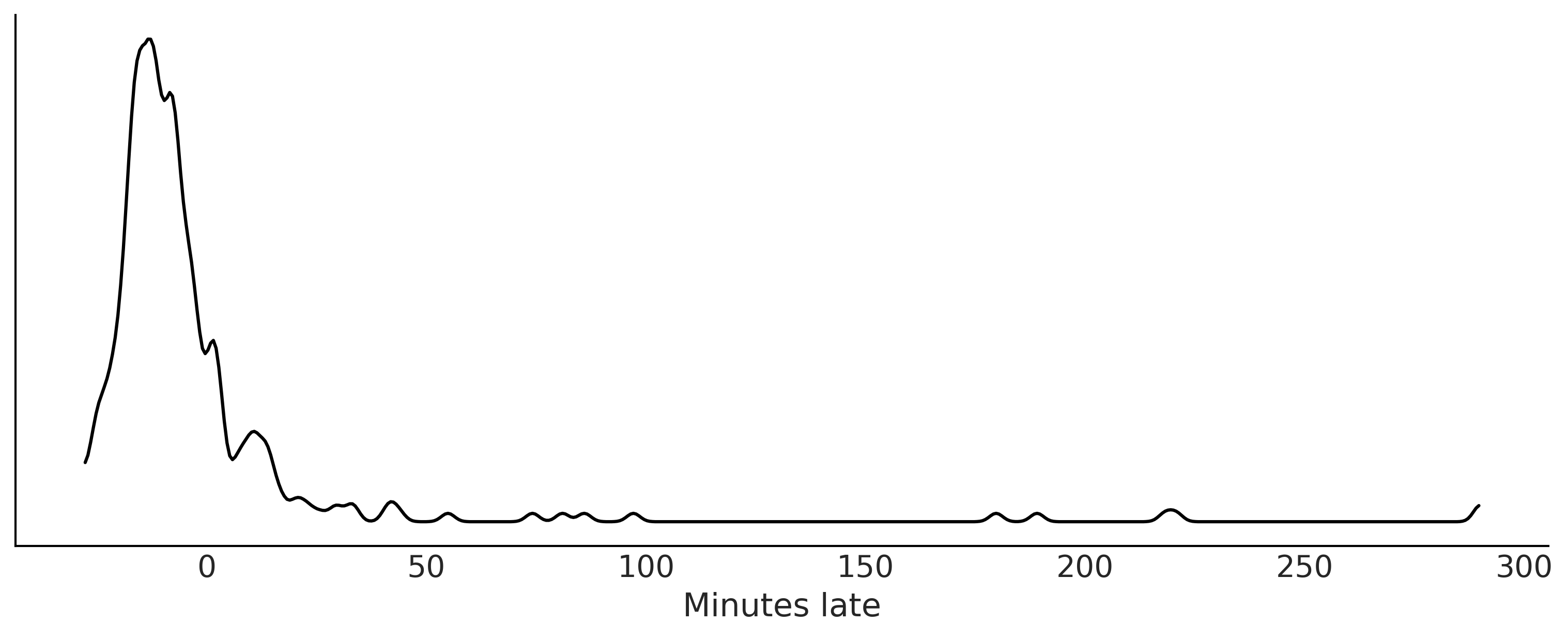
Code 9.1 and Figure 9.2#

df = pd.read_csv("../data/948363589_T_ONTIME_MARKETING.zip", low_memory=False)

fig, ax = plt.subplots(figsize=(10,4))
msn_arrivals = df[(df["DEST"] == 'MSN') & df["ORIGIN"]
                  .isin(["MSP", "DTW"])]["ARR_DELAY"]

az.plot_kde(msn_arrivals.values, ax=ax)
ax.set_yticks([])
ax.set_xlabel("Minutes late")
plt.savefig('img/chp09/arrivaldistributions.png')

../_images/d4b50670c56199fb9f93c206542fc2348c50e206cdf2a1fe0f96fafa94419b19.png

msn_arrivals.notnull().value_counts()

True    336
Name: ARR_DELAY, dtype: int64

Code 9.2#

try:
    # This is the real code, just try except block to allow for the whole notebook tor execute
    with pm.Model() as normal_model:
        normal_mu = ...
        normal_sd = ...

        normal_delay = pm.SkewNormal("delays", mu=normal_mu,
                                     sd=normal_sd, observed=msn_arrivals)

    with pm.Model() as skew_normal_model:
        skew_normal_alpha = ...
        skew_normal_mu = ...
        skew_normal_sd = ...

        skew_normal_delays = pm.SkewNormal("delays", mu=skew_normal_mu, sd=skew_normal_sd,
                                           alpha=skew_normal_alpha, observed=msn_arrivals)


    with pm.Model() as gumbel_model:
        gumbel_beta = ...
        gumbel_mu = ...

        gumbel_delays = pm.Gumbel("delays", mu=gumbel_mu,
                                  beta=gumbel_beta, observed=msn_arrivals)
except:
    pass

Choosing Priors and Predictive Priors#

Code 9.3#

samples = 1000

with pm.Model() as normal_model:
    normal_sd = pm.HalfStudentT("sd",sigma=60, nu=5)
    normal_mu = pm.Normal("mu", 0, 30) 

    normal_delay = pm.Normal("delays", mu=normal_mu, sd=normal_sd, observed=msn_arrivals)
    normal_prior_predictive = pm.sample_prior_predictive()
    
with pm.Model() as gumbel_model:
    gumbel_beta = pm.HalfStudentT("beta", sigma=60, nu=5)
    gumbel_mu = pm.Normal("mu", 0, 20)
    
    gumbel_delays = pm.Gumbel("delays", mu=gumbel_mu, beta=gumbel_beta, observed=msn_arrivals)
    gumbel_predictive = pm.sample_prior_predictive()

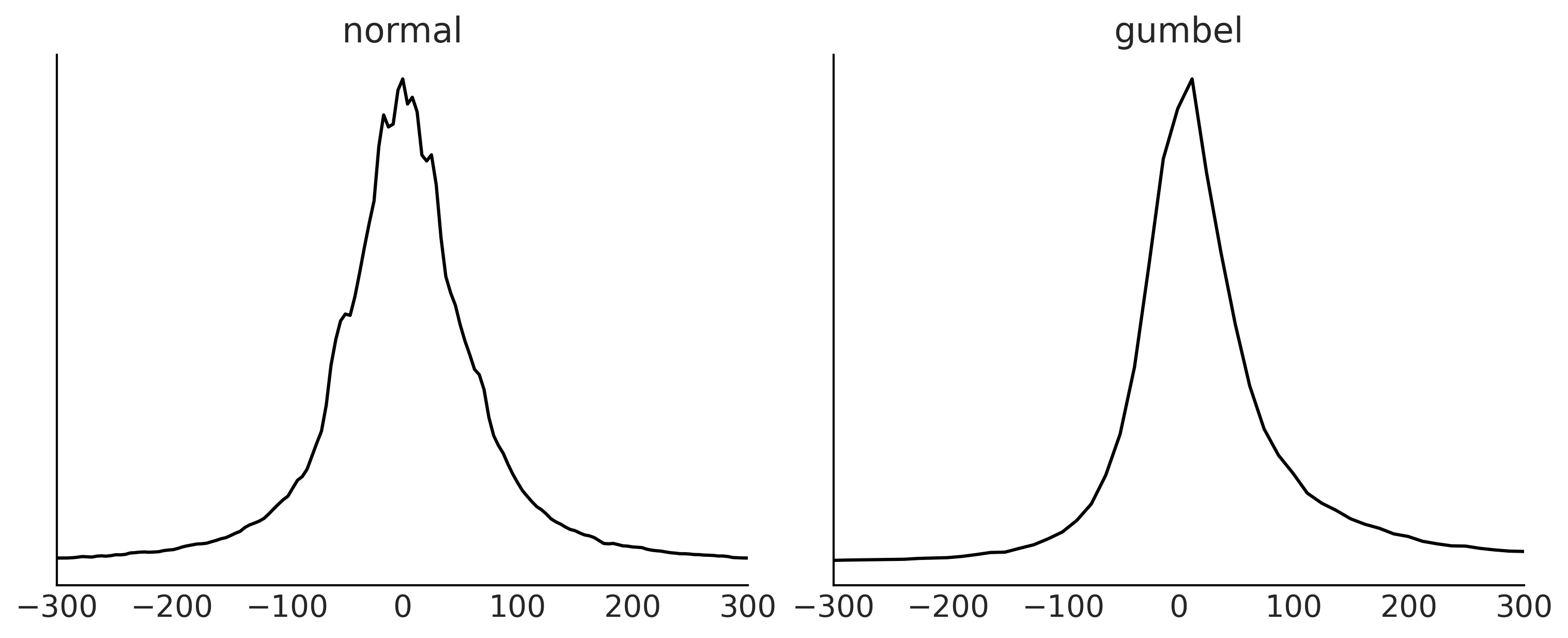
Figure 9.3#

fig, axes = plt.subplots(1, 2, figsize=(10, 4))

prior_predictives = {"normal":normal_prior_predictive, "gumbel": gumbel_predictive }

for i, (label, prior_predictive) in enumerate(prior_predictives.items()):
    
    data = prior_predictive["delays"].flatten()
    az.plot_dist(data, ax=axes[i])
    axes[i].set_yticks([])
    axes[i].set_xlim(-300, 300)
    axes[i].set_title(label)
    
fig.savefig("img/chp09/Airline_Prior_Predictive.png")

../_images/96ebd5ad2fd1e3cd9401e922902d947279b0d6f0804ce8ab23fbf28743b97b17.png

Inference and Inference Diagnostics#

Code 9.4#

with normal_model:
    normal_delay_trace = pm.sample(random_seed=0, chains=2)
    az.plot_rank(normal_delay_trace)
plt.savefig('img/chp09/rank_plot_bars_normal.png')

/tmp/ipykernel_141130/700159645.py:2: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
  normal_delay_trace = pm.sample(random_seed=0, chains=2)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 4 jobs)
NUTS: [mu, sd]

100.00% [4000/4000 00:01<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 1 seconds.

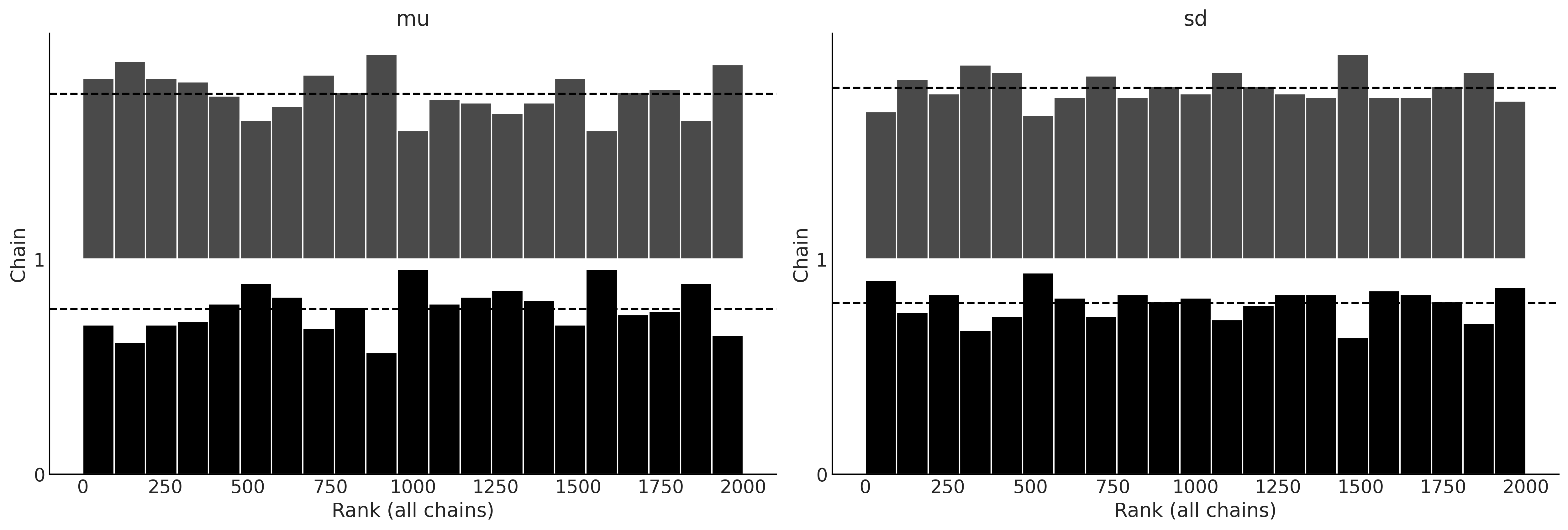
../_images/d3df22f4fcbf601b90423ad9fa383c94f482e59f0022a940183b5e390100b090.png

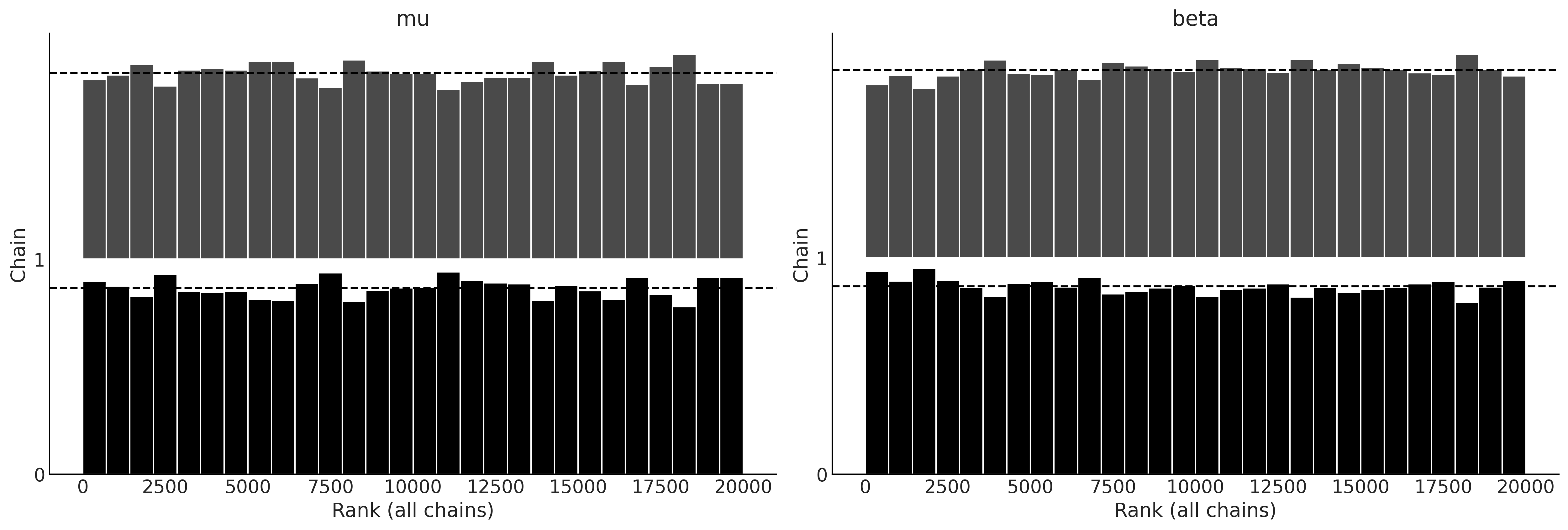
Figure 9.5#

with gumbel_model:
    gumbel_delay_trace = pm.sample(random_seed=0, chains=2, draws=10000)
    az.plot_rank(gumbel_delay_trace)
plt.savefig('img/chp09/rank_plot_bars_gumbel.png')

/tmp/ipykernel_141130/173437934.py:2: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
  gumbel_delay_trace = pm.sample(random_seed=0, chains=2, draws=10000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 4 jobs)
NUTS: [mu, beta]

100.00% [22000/22000 00:05<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 10_000 draw iterations (2_000 + 20_000 draws total) took 5 seconds.

../_images/4a3972bc5223fac991fbe6ad1976297f158458d34a7239355d4f97bdc1f734fb.png

Posterior Plots#

Figure 9.6#

az.plot_posterior(normal_delay_trace)
plt.savefig('img/chp09/posterior_plot_delays_normal.png');

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

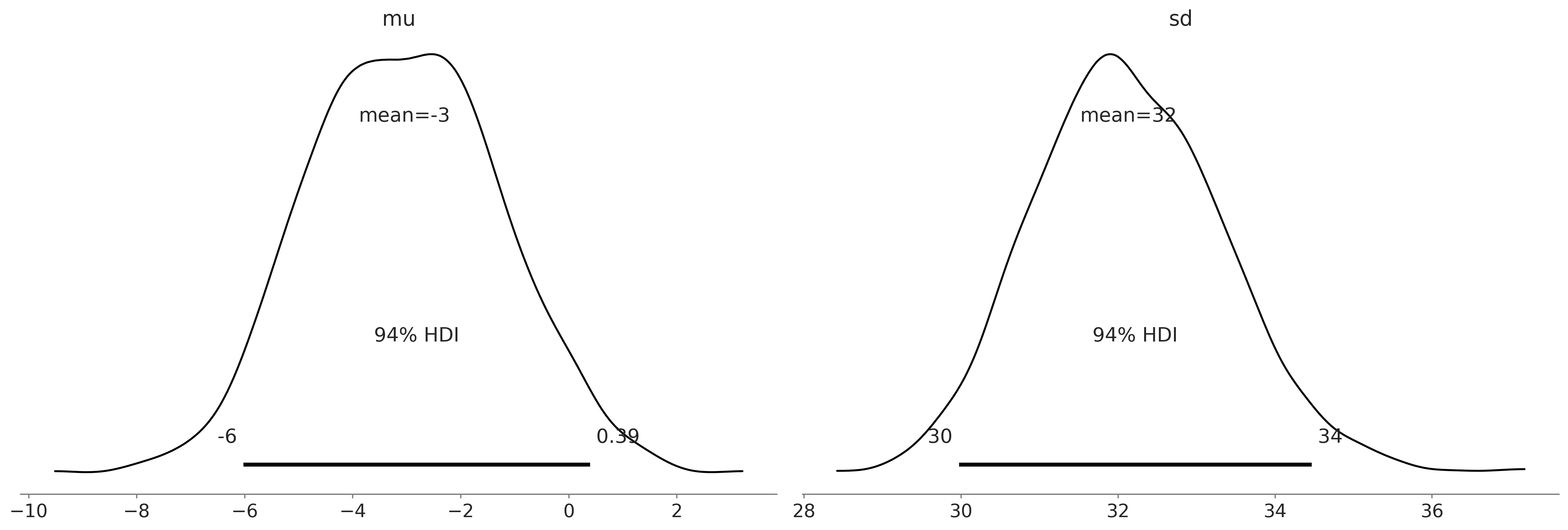
../_images/dd8060e8f6e39b1780fb352a433fbbcb4932a9694032c79e41ec53488f3f1650.png

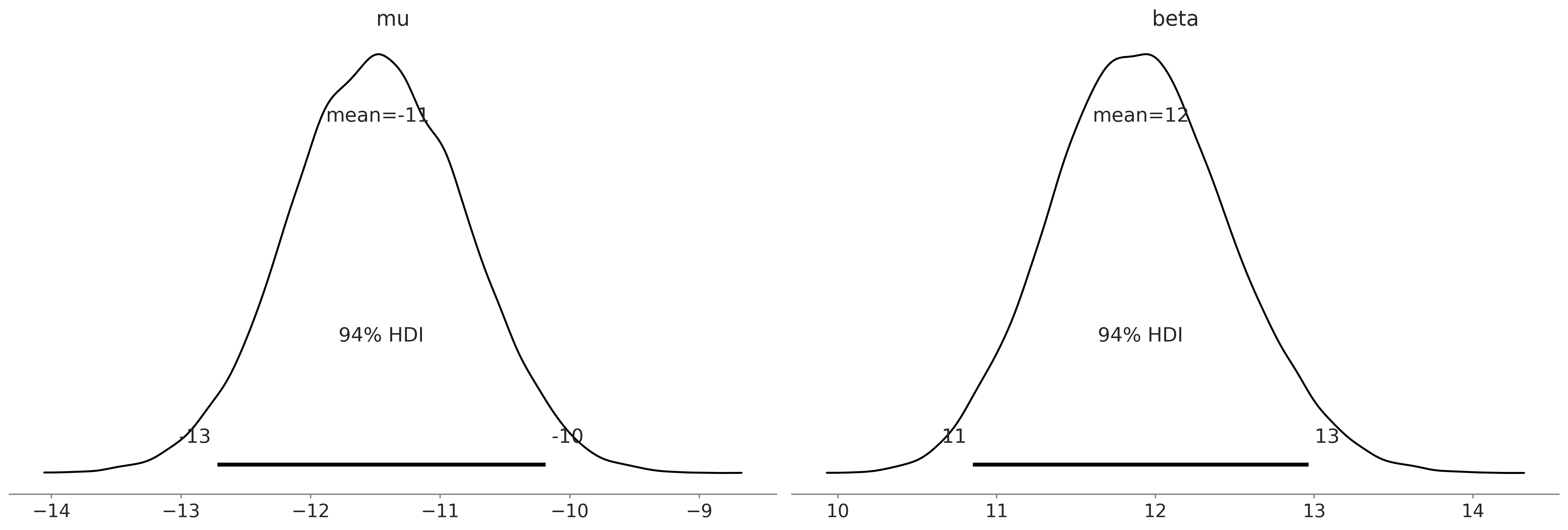
Figure 9.7#

az.plot_posterior(gumbel_delay_trace)
plt.savefig('img/chp09/posterior_plot_delays_gumbel.png');

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

../_images/1df818026ee55923f390c5f67f8b531210324650cc4c34452af7aeab80c8aac1.png

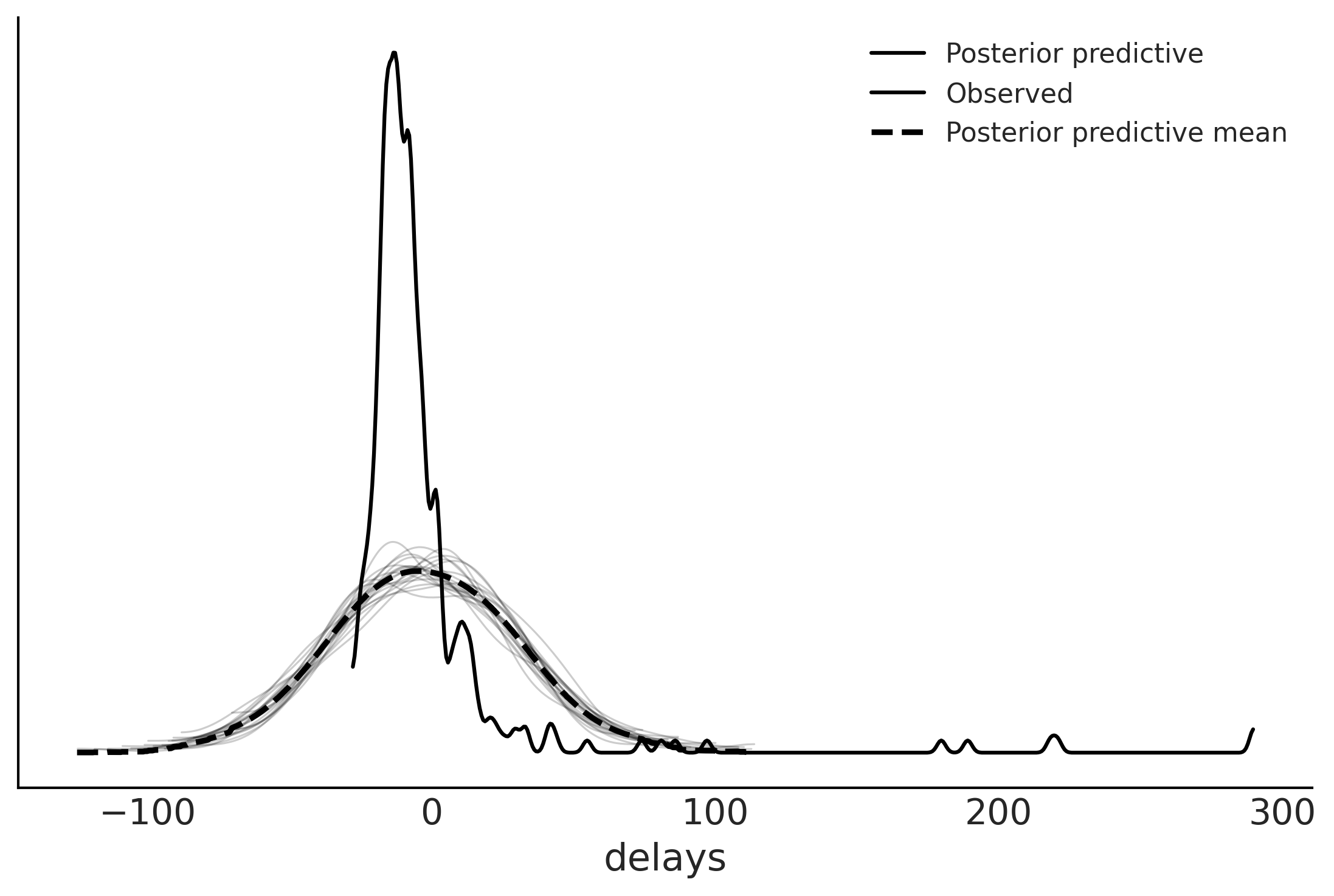
Evaluating Posterior Predictive Distributions#

Code 9.5#

with normal_model:
    normal_delay_trace = pm.sample(random_seed=0)
    normal_post_pred_check = pm.sample_posterior_predictive(normal_delay_trace, random_seed=0)
    normal_data = az.from_pymc3(trace=normal_delay_trace, posterior_predictive=normal_post_pred_check)

/tmp/ipykernel_141130/2703936732.py:2: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
  normal_delay_trace = pm.sample(random_seed=0)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sd]

100.00% [8000/8000 00:01<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

100.00% [4000/4000 00:02<00:00]

fig, ax = plt.subplots()
az.plot_ppc(normal_data, observed=True, num_pp_samples=20, ax=ax)

array([<AxesSubplot:xlabel='delays'>], dtype=object)

../_images/82e6f69706e56a5b033fb5aee7ac953b8fff8206483d713917a110d34ecef02c.png

Gumbel Posterior Predictive#

with gumbel_model:
    gumbel_post_pred_check = pm.sample_posterior_predictive(gumbel_delay_trace, random_seed=0)
    gumbel_data = az.from_pymc3(trace=gumbel_delay_trace, posterior_predictive=gumbel_post_pred_check)

100.00% [20000/20000 00:05<00:00]

Figure 9.8#

fig, ax = plt.subplots(2,1, sharex=True)

az.plot_ppc(normal_data, observed=False, num_pp_samples=20, ax=ax[0], color="C4")
az.plot_kde(msn_arrivals, ax=ax[0], label="Observed");

az.plot_ppc(gumbel_data, observed=False, num_pp_samples=20, ax=ax[1], color="C4")
az.plot_kde(msn_arrivals, ax=ax[1], label="Observed");
ax[0].set_title("Normal")
ax[0].set_xlabel("")
ax[1].set_title("Gumbel")
ax[1].legend().remove()
plt.savefig("img/chp09/delays_model_posterior_predictive.png")

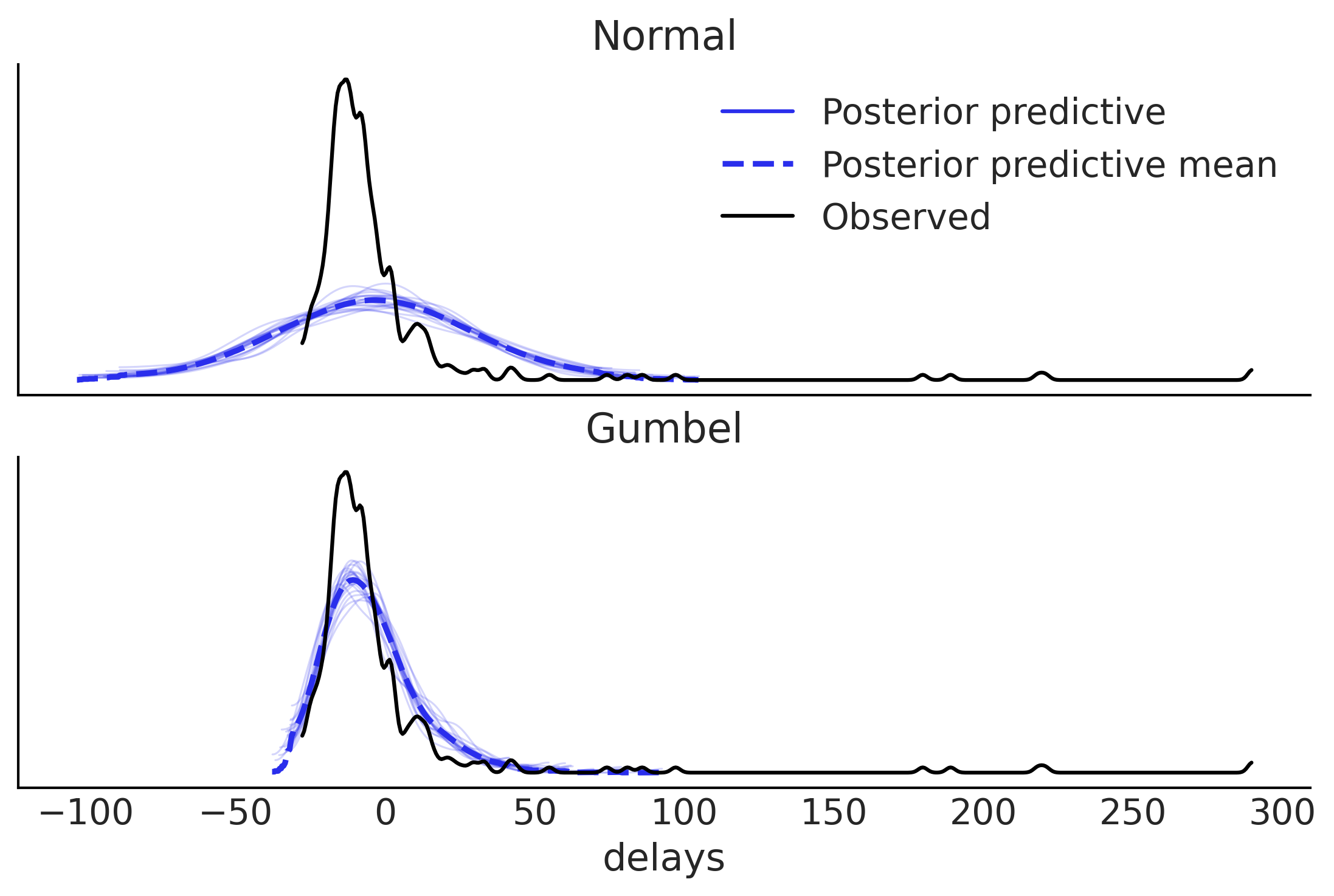
../_images/4f0c358a694a6a0097059f8cb7f5096bc364b1b7406ec3c417070a9253b29e97.png

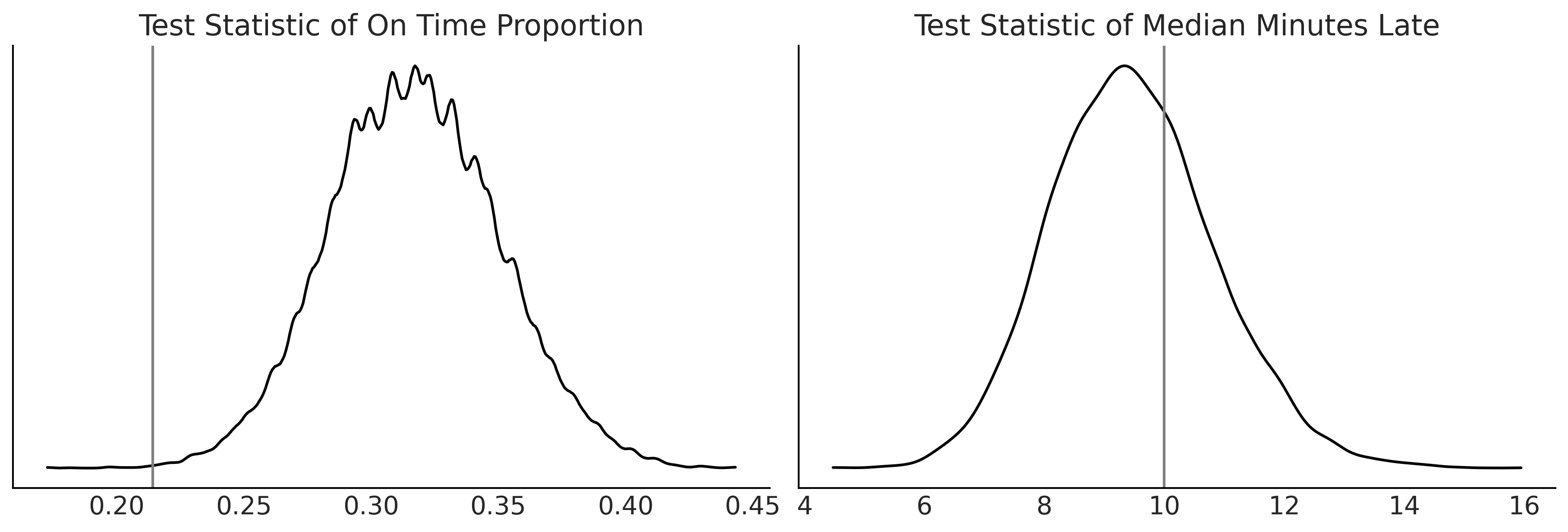
Figure 9.9#

gumbel_late = gumbel_data.posterior_predictive["delays"].values.reshape(-1, 336).copy()
dist_of_late = (gumbel_late > 0).sum(axis=1) / 336

fig, axes = plt.subplots(1,2, figsize=(12,4))

gumbel_late = gumbel_data.posterior_predictive["delays"].values.reshape(-1, 336).copy()
dist_of_late = (gumbel_late > 0).sum(axis=1) / 336
az.plot_dist(dist_of_late, ax=axes[0])

percent_observed_late = (msn_arrivals > 0).sum() / 336
axes[0].axvline(percent_observed_late, c="gray")
axes[0].set_title("Test Statistic of On Time Proportion")
axes[0].set_yticks([])


gumbel_late[gumbel_late < 0] = np.nan
median_lateness = np.nanmedian(gumbel_late, axis=1)
az.plot_dist(median_lateness,  ax=axes[1])

median_time_observed_late = msn_arrivals[msn_arrivals >= 0].median()
axes[1].axvline(median_time_observed_late, c="gray")
axes[1].set_title("Test Statistic of Median Minutes Late")
axes[1].set_yticks([])

plt.savefig("img/chp09/arrival_test_statistics_for_gumbel_posterior_predictive.png")

../_images/70c88fefada1ab33536c7d022d4ef6a10562d365535c42677a63873b6e2f47d6.png

Model Comparison#

Code 9.6#

compare_dict = {"normal": normal_data,"gumbel": gumbel_data}
comp = az.compare(compare_dict, ic="loo")
comp

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:145: UserWarning: The default method used to estimate the weights for each model,has changed from BB-pseudo-BMA to stacking
  warnings.warn(
/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:655: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

	rank	loo	p_loo	d_loo	weight	se	dse	warning	loo_scale
gumbel	0	-1410.341706	5.846255	0.000000	1.000000e+00	45.130865	0.000000	False	log
normal	1	-1653.653643	21.616843	243.311937	1.761862e-10	65.189335	27.416848	True	log

Figure 9.10#

_, axes = plt.subplots(1, 2, figsize=(12, 4), sharey=True)
for label, model, ax in zip(("gumbel", "normal"),(gumbel_data, normal_data), axes):
    az.plot_loo_pit(model, y="delays", legend=False, use_hdi=True, ax=ax)
    ax.set_title(label)
    
plt.savefig('img/chp09/loo_pit_delays.png')

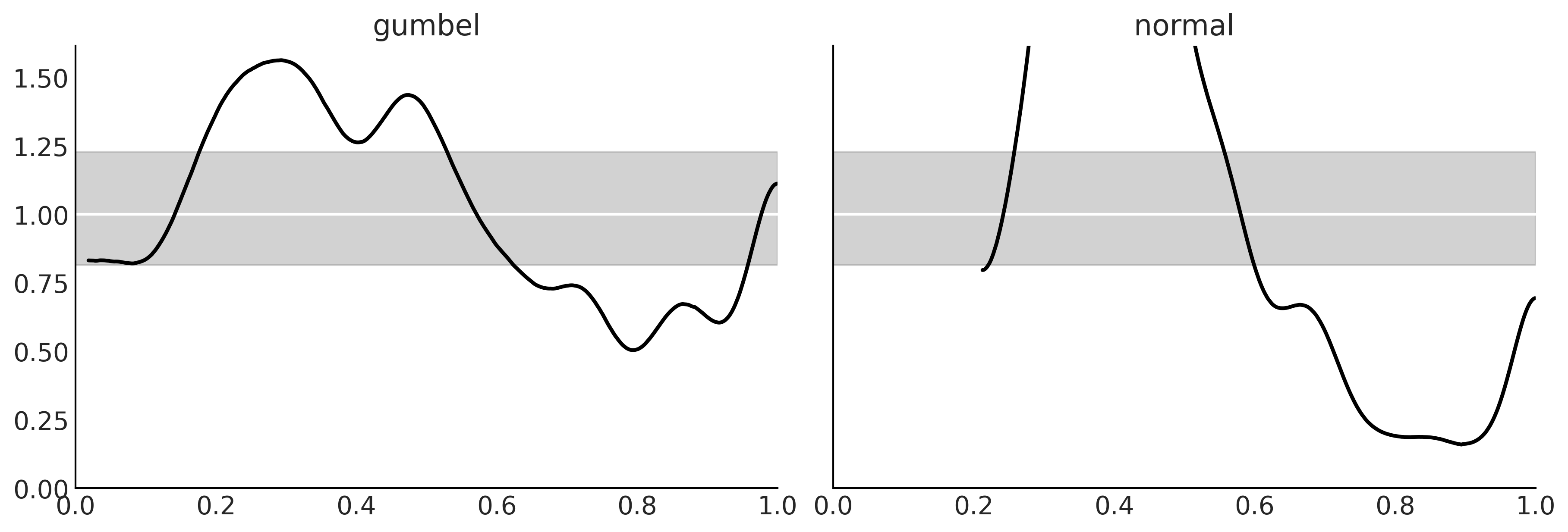
../_images/3df62d9fe5f4e1a081b383ade9905b69eebaa75337a6f9ad908aaee99be254e1.png

Table 9.1#

cmp_dict = {"gumbel": gumbel_data,
            "normal": normal_data}
            
cmp = az.compare(cmp_dict)
cmp

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:145: UserWarning: The default method used to estimate the weights for each model,has changed from BB-pseudo-BMA to stacking
  warnings.warn(
/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:655: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

	rank	loo	p_loo	d_loo	weight	se	dse	warning	loo_scale
gumbel	0	-1410.341706	5.846255	0.000000	1.000000e+00	45.130865	0.000000	False	log
normal	1	-1653.653643	21.616843	243.311937	1.761862e-10	65.189335	27.416848	True	log

Code 9.7 and Figure 9.12#

az.plot_compare(cmp)
plt.savefig("img/chp09/model_comparison_airlines.png")

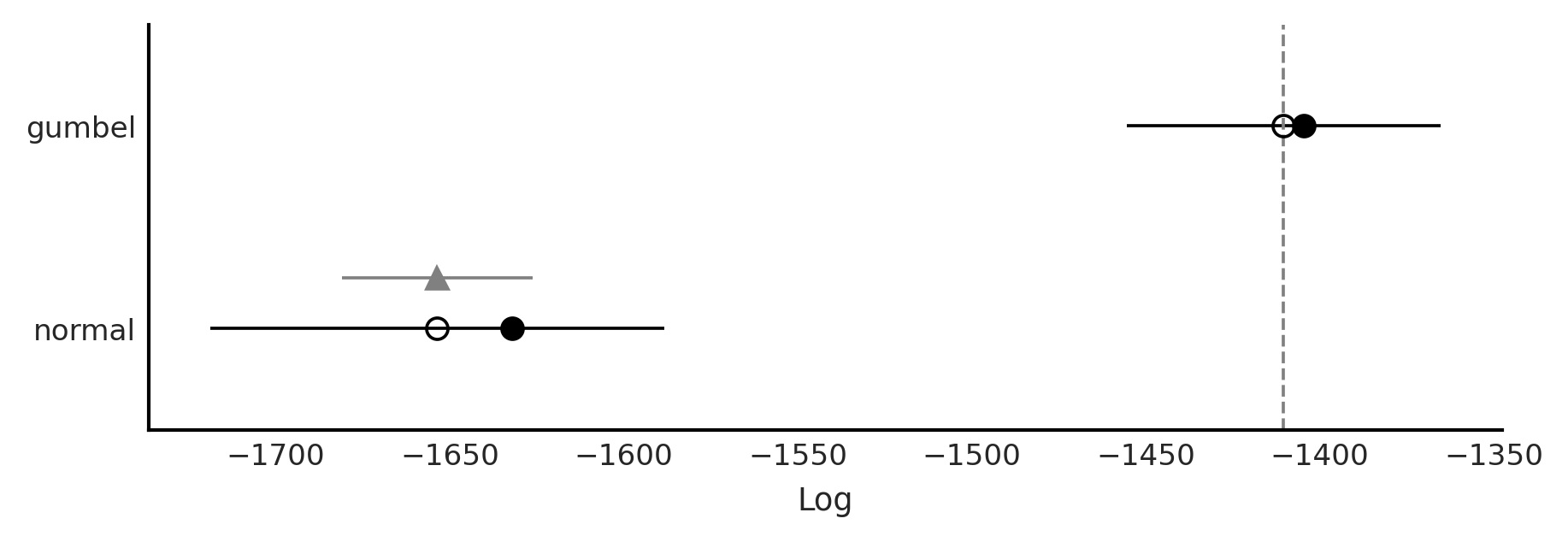
../_images/af1c067cc36d304fc8c6e89d0de92bafe0dabd80ede40afdd328149b1ed49934.png

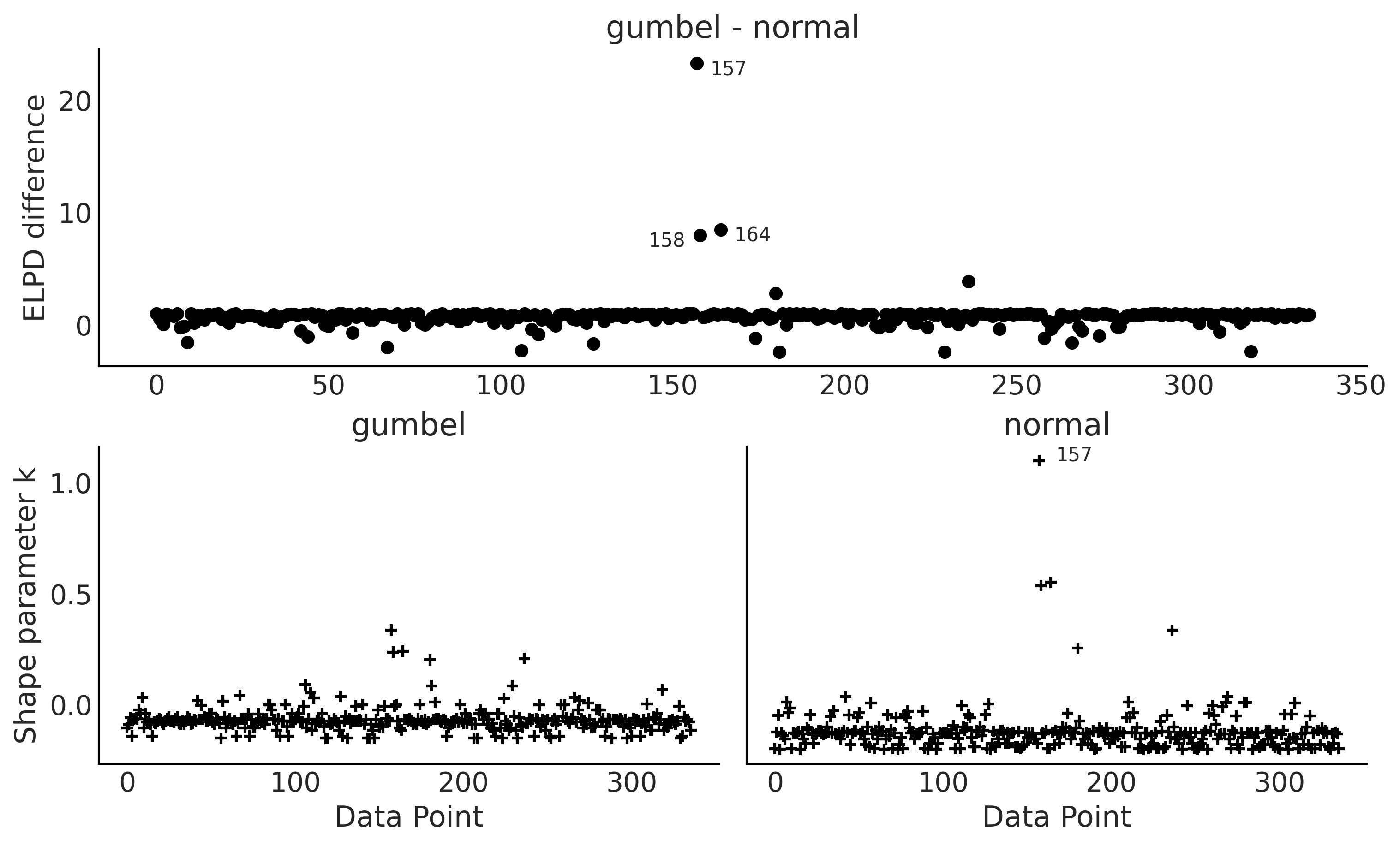
Figure 9.12#

gumbel_loo = az.loo(gumbel_data, pointwise=True)
normal_loo = az.loo(normal_data, pointwise=True)

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:655: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

fig = plt.figure(figsize=(10, 6))
gs = fig.add_gridspec(2, 2)

ax = fig.add_subplot(gs[0, :])
ax1 = fig.add_subplot(gs[1, 0])
ax2 = fig.add_subplot(gs[1, 1])


diff = gumbel_loo.loo_i - normal_loo.loo_i
idx = np.abs(diff) > 4
x_values = np.where(idx)[0]
y_values = diff[idx].values
az.plot_elpd(cmp_dict, ax=ax)

for x, y, in zip(x_values, y_values):
    if x != 158:
        x_pos = x+4
    else:
        x_pos = x-15
    ax.text(x_pos, y-1, x)
    
for label, elpd_data, ax in zip(("gumbel", "normal"),
                                (gumbel_loo, normal_loo), (ax1, ax2)):
    az.plot_khat(elpd_data, ax=ax)
    ax.set_title(label)
    idx = elpd_data.pareto_k > 0.7
    x_values = np.where(idx)[0]
    y_values = elpd_data.pareto_k[idx].values
    for x, y, in zip(x_values, y_values):
        if x != 158:
            x_pos = x+10
        else:
            x_pos = x-30
        ax.text(x_pos, y, x)
    

#     ttl = ax.title
#    ttl.set_position([.5, 10])

ax1.set_ylim(ax2.get_ylim())
ax2.set_ylabel("")
ax2.set_yticks([])
plt.savefig('img/chp09/elpd_plot_delays.png');

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/stats/stats.py:655: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

../_images/03479b1fc73abb519acc4f0f23864c969182847745e7aa8618132f8c81f4e1f0.png

Reward Functions and Decisions#

posterior_pred = gumbel_data.posterior_predictive["delays"].values.reshape(-1, 336).copy()

Code 9.8#

@np.vectorize
def current_revenue(delay):
    """Calculates revenue """
    if delay >= 0:
        return 300*delay
    return np.nan

Code 9.9#

def revenue_calculator(posterior_pred, revenue_func):    
    revenue_per_flight = revenue_func(posterior_pred)
    average_revenue = np.nanmean(revenue_per_flight)
    return revenue_per_flight, average_revenue

revenue_per_flight, average_revenue = revenue_calculator(posterior_pred, current_revenue)
average_revenue

3930.8899204759587

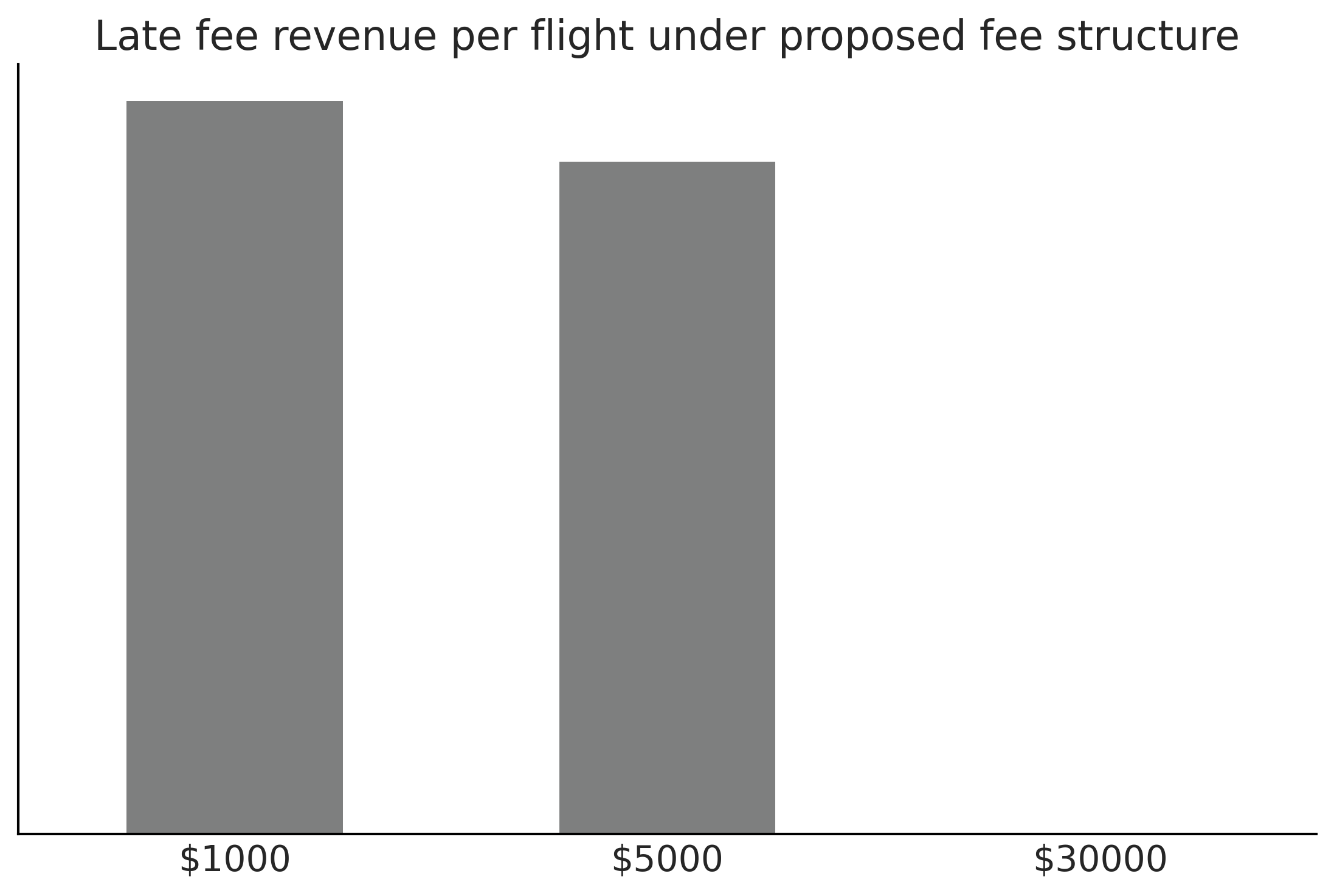
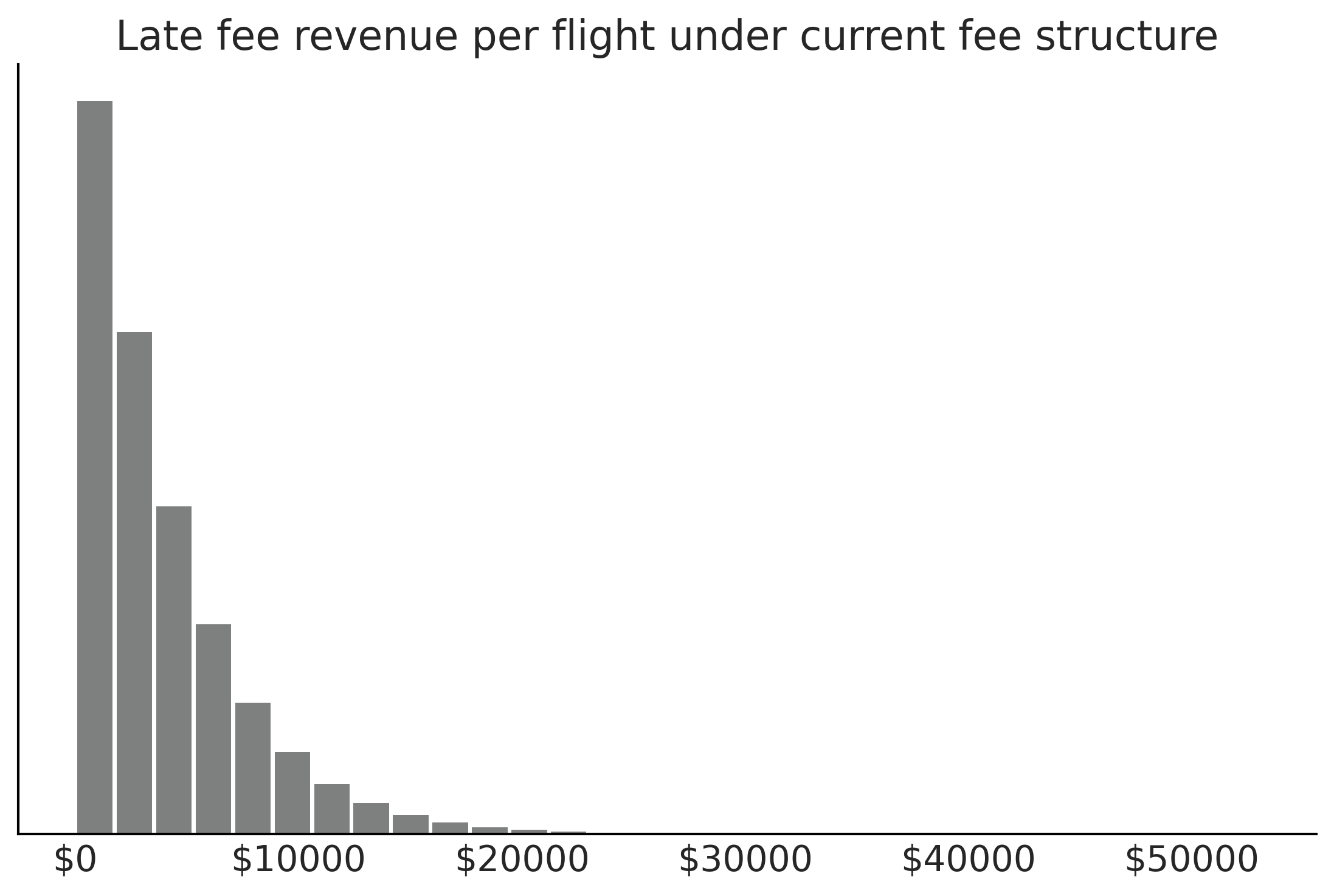
Figure 9.13#

fig, ax = plt.subplots()
ax.hist(revenue_per_flight.flatten(), bins=30, rwidth=.9, color="C2" )
ax.set_yticks([])
ax.set_title("Late fee revenue per flight under current fee structure")
ax.xaxis.set_major_formatter('${x:1.0f}')
plt.savefig("img/chp09/late_fee_current_structure_hist.png")

../_images/bf65c7b6358dc7a8b5d6a02e3caf66534a78f4c2e948b6680f9359bba5d06c0e.png

Code 9.10#

@np.vectorize
def proposed_revenue(delay):
    """Calculates revenue """
    if delay >= 100:
        return 30000
    elif delay >= 10:
        return 5000
    elif delay >= 0:
        return 1000
    else:
        return np.nan

revenue_per_flight_proposed, average_revenue_proposed = revenue_calculator(posterior_pred, proposed_revenue)
average_revenue_proposed

2921.977902254481

Experimental Example: Comparing Between Two Groups#

composites_df = pd.read_csv("../data/CompositeTensileTest.csv")

unidirectional = composites_df["Unidirectional Ultimate Strength (ksi)"].values
bidirectional = composites_df["Bidirectional Ultimate Strength (ksi)"].values

Code 9.11#

with pm.Model() as unidirectional_model:
    sd = pm.HalfStudentT("sd_uni", 20)
    mu = pm.Normal("mu_uni", 120, 30)
    
    uni_ksi = pm.Normal("uni_ksi", mu=mu, sd=sd, observed=unidirectional)
    
    # prior_uni = pm.sample_prior_predictive()
    trace = pm.sample(draws=5000)
    
uni_data = az.from_pymc3(trace=trace)

/tmp/ipykernel_141130/4059400571.py:8: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
  trace = pm.sample(draws=5000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_uni, sd_uni]

100.00% [24000/24000 00:03<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 4 seconds.
/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

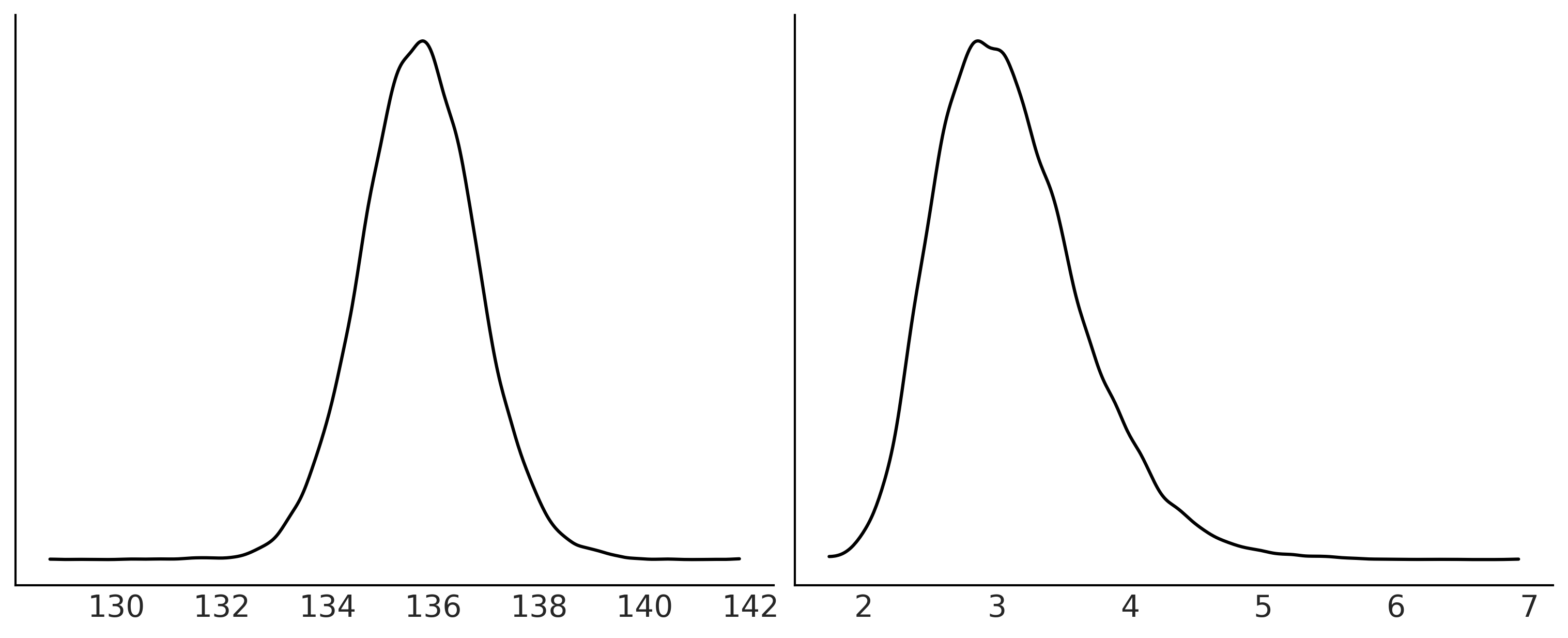
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
az.plot_kde(uni_data.posterior["mu_uni"], ax=axes[0]);
az.plot_kde(uni_data.posterior["sd_uni"], ax=axes[1]);
axes[0].set_yticks([])
axes[1].set_yticks([])
fig.savefig("img/chp09/kde_uni.png")

../_images/d060c595f636317f29b565348a05b4719b74b45621b188ebed6b5e61ef1ca301.png

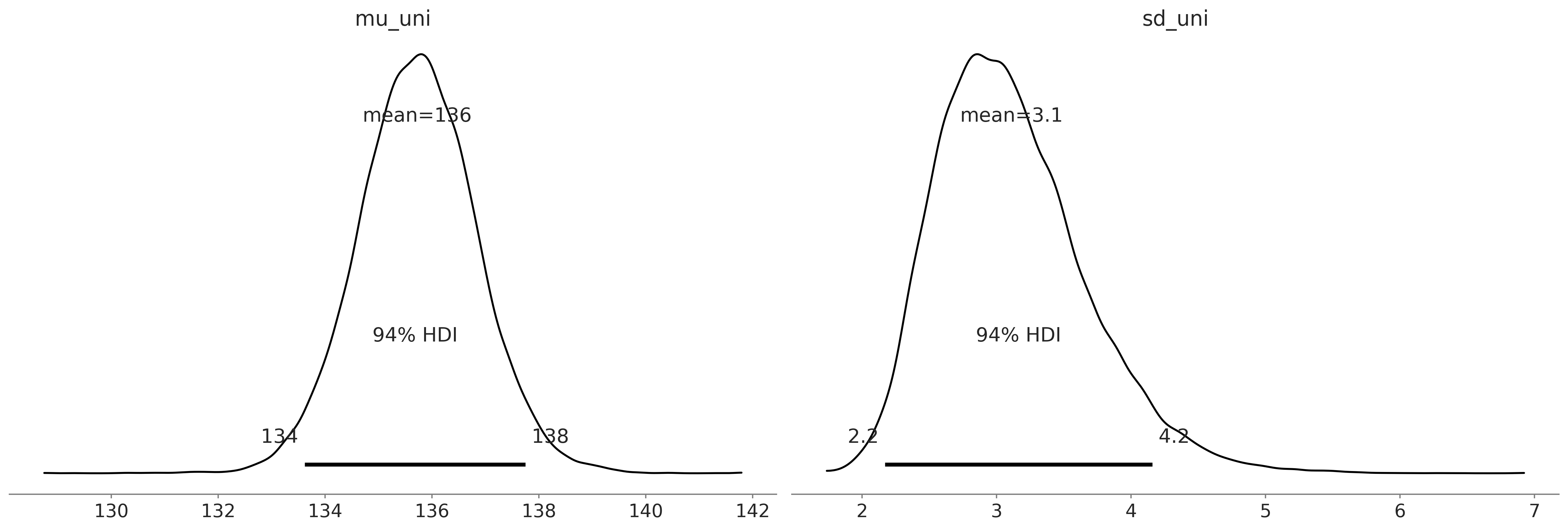
Code 9.12 and Figure 9.15#

az.plot_posterior(uni_data);
plt.savefig("img/chp09/posterior_uni.png")

../_images/b06a738fe7c1d5b1bc6ca4a010404dcf9aa0a1881dc05df3bf962f3a4337dc6f.png

Code 9.13#

μ_m = 120
μ_s = 30

σ_low = 10
σ_high = 30

with pm.Model() as model:
    uni_mean = pm.Normal('uni_mean', mu=μ_m, sd=μ_s)
    bi_mean = pm.Normal('bi_mean', mu=μ_m, sd=μ_s)
    
    uni_std = pm.Uniform('uni_std', lower=σ_low, upper=σ_high)
    bi_std = pm.Uniform('bi_std', lower=σ_low, upper=σ_high)
    
    ν = pm.Exponential('ν_minus_one', 1/29.) + 1
    
    λ1 = uni_std**-2
    λ2 = bi_std**-2

    group1 = pm.StudentT('uni', nu=ν, mu=uni_mean, lam=λ1, observed=unidirectional)
    group2 = pm.StudentT('bi', nu=ν, mu=bi_mean, lam=λ2, observed=bidirectional)
    
    diff_of_means = pm.Deterministic('Difference of Means', uni_mean - bi_mean)
    diff_of_stds = pm.Deterministic('Difference of Stds', uni_std - bi_std)
    effect_size = pm.Deterministic('Effect Size',
                                   diff_of_means / np.sqrt((uni_std**2 + bi_std**2) / 2))
    
    t_trace = pm.sample(draws=10000)

compare_data = az.from_pymc3(trace)

/tmp/ipykernel_141130/3744684942.py:27: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
  trace = pm.sample(draws=10000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [ν_minus_one, bi_std, uni_std, bi_mean, uni_mean]

100.00% [44000/44000 00:10<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 12 seconds.
/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

Code 9.14#

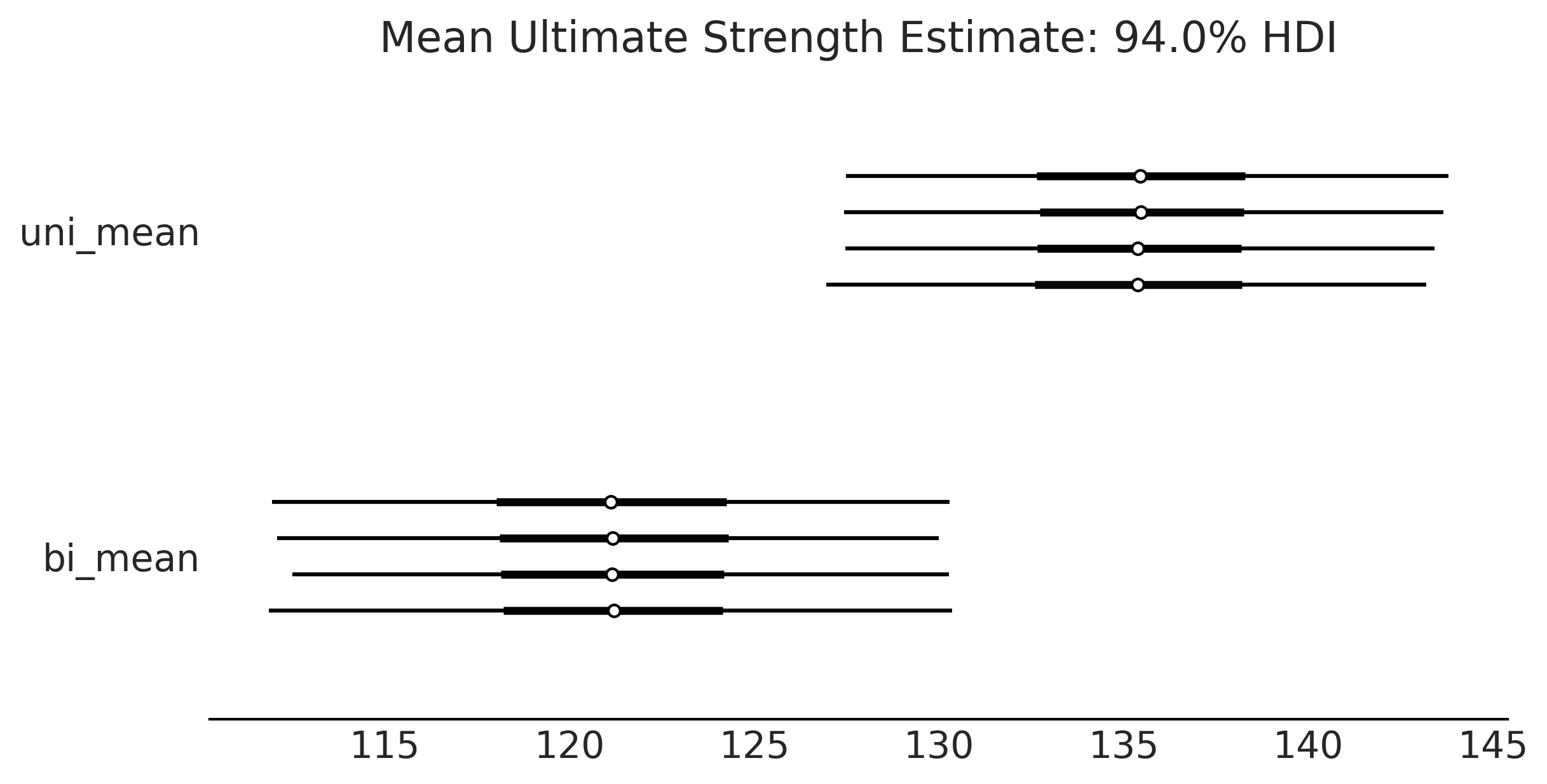
axes = az.plot_forest(trace, var_names=['uni_mean','bi_mean'], figsize=(8, 4));
axes[0].set_title("Mean Ultimate Strength Estimate: 94.0% HDI")
plt.savefig("img/chp09/Posterior_Forest_Plot.png")

../_images/ecea51ef7ed0a7a2687aa908208fbf12eb65b8bd09526e5a281b95a6baa0e83b.png

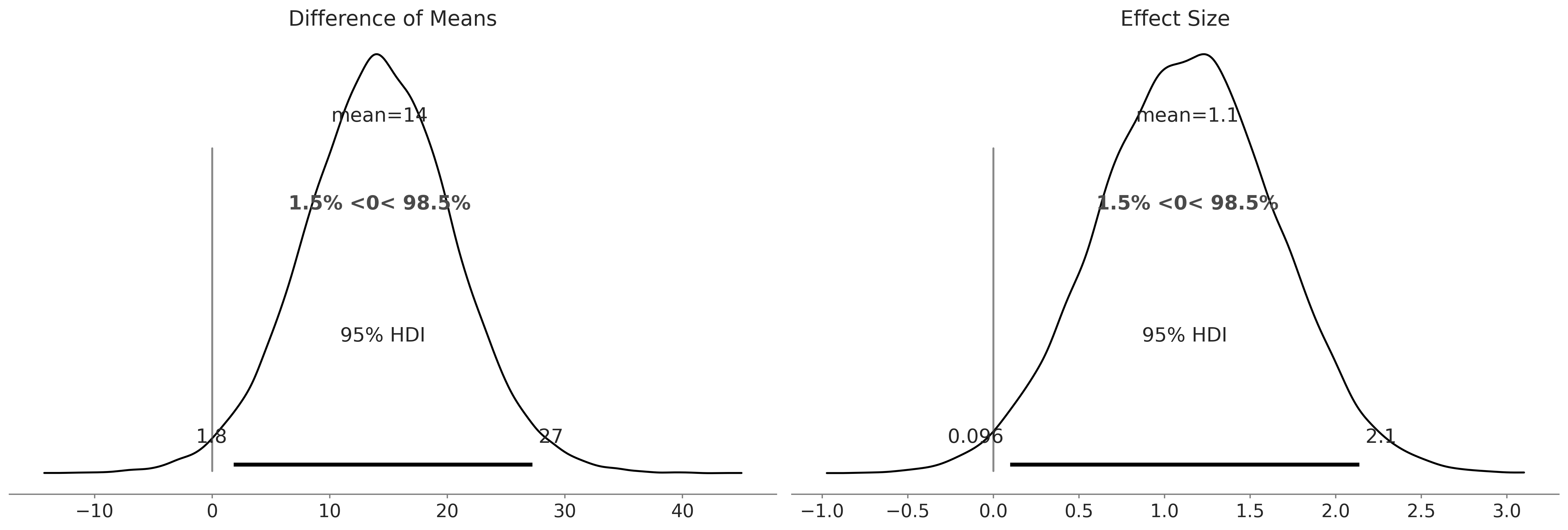
Code 9.15 and Figure 9.17#

az.plot_posterior(trace, var_names=['Difference of Means','Effect Size'], hdi_prob=.95, ref_val=0);
plt.savefig("img/chp09/composite_difference_of_means.png")

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

../_images/ccfe2e83caae0aa3591bf45afce230a3c63a12bf368b91c3e917bf58bcd428bd.png

Code 9.16#

az.summary(t_trace, kind="stats")

/home/canyon/miniconda3/envs/bmcp/lib/python3.9/site-packages/arviz/data/io_pymc3.py:96: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  warnings.warn(

	mean	sd	hdi_3%	hdi_97%
uni_mean	135.419	4.302	127.457	143.675
bi_mean	121.188	4.806	112.111	130.283
uni_std	12.197	2.450	10.000	16.550
bi_std	13.268	3.229	10.000	19.283
ν_minus_one	36.507	30.447	0.218	92.225
Difference of Means	14.232	6.434	1.831	26.158
Difference of Stds	-1.071	4.073	-9.935	6.548
Effect Size	1.133	0.522	0.127	2.083